Corsi precedenti

Soluzione commentata

La classe ListNode

class ListNode {
	int info;
	ListNode prev;
	ListNode next;
}

La classe ListaCollegata (senza MergeSort)

public class ListaCollegata {
    private ListNode first;
    private ListNode last;
 
    public ListaCollegata() {
        first=last=null;
    }
 
    public void inserisciInCoda(int info) {
        ListNode l=new ListNode();
        l.info=info;
        if(first==null) {
            l.prev=l.next=null;
            first=last=l;
        } else {
            l.prev=last;
            l.next=null;
            last.next=l;
            last=l;
        }
    }
 
    public String toString() {
        ListNode l=first;
        String s=new String();
        while(l!=null) {
            s=s+l.info;
            l=l.next;
            if(l!=null)
                s=s+", ";
        }
        return s;
    }
}

Il MergeSort

Per prima cosa leggi i suggerimenti dell’esercitazione.

Il metodo ricorsivo mergeSort prende in input gli estremi della sottolista da ordinare; tali estremi sono riferimenti a ListNode:

private ListNode mergeSortRic(ListNode i, ListNode f) {
    ....
}

Il motivo per cui il metodo restituisce un ListNode sarà chiarito in seguito.

Nel caso ricorsivo (i != f), la lista è spezzata in due parti uguali. Per trovare l’elemento medio, avviciniamo i riferimenti i ed f, facendo avanzare i e retrocedere f, fino a farli incontrare. Questa operazione è svolta dal metodo seguente:

private ListNode trovaMeta(ListNode i, ListNode f) {
    boolean pari=true;
    while(i!=f) {
        if(pari)
            i=i.next;
        else
            f=f.prev;
        pari = !pari;
    }
    return i;
}

Osservare che nelle iterazioni pari avanziamo i, in quelle dispari retrocediamo f.

Osserviamo che il costo di un’invocazione di trovaMeta è O(|l(i, f)|), dove con l(i, f) indichiamo la sottolista compresa tra il nodo i e il nodo f. Tale costo è asintoticamente uguale al costo del successivo passo merge, per cui l’invocazione del metodo trovaMeta non aumenta il costo asintotico dell’algoritmo.

Ora dobbiamo invocare il MergeSort ricorsivamente sulle due sottoliste individuate l(i, m.prev) e l(p, f), e fondere le due liste restituiteci. Ricordiamoci, però, che le due liste restituite non hanno necessariamente come primi elementi i e p. Occorre che le chiamate ricorsive di MergeSort ci restituiscano il nuovo primo elemento delle liste ordinate. Ecco il significato dell’oggetto di tipo ListNode restituitoci dalla chiamata ricorsiva.

Per comodità supponiamo, altresì, che le sottoliste restituiteci siano “liste” vere e proprie, cioè che l’ultimo nodo abbia null come riferimento al nodo successivo, e il primo nodo abbia null come riferimento al precedente.

Ecco le chiamate ricorsive:

ListNode m = trovaMeta(i, f);
ListNode i1 = mergeSortRic(i, m.prev);
ListNode i2 = mergeSortRic(m, f);

Ora i1 e i2 puntano alle due liste ordinate, da fondere. Il primo elemento della lista fusa sarà quello che contiene l’intero più basso tra l’elemento puntato da i1 e quello puntato da i2: troviamolo e mettiamolo in i:

if(i1.info < i2.info) {
    i=i1;
    i1=i1.next;
}   else {
    i=i2;
    i2=i2.next;
}
i.prev=null;

Osserviamo che, correttamente, abbiamo impostato il riferimento all’elemento precedente il primo a null. Ed ora fondiamo le due liste, usando il riferimento p (inizializzato a i) per scandire la lista fusa, e i1, i2 per scandire le due liste ancora da fondere:

ListNode p=i;
while(i1!=null || i2!=null) {
    if(i1!=null && i2!=null) {
        if(i1.info < i2.info) {
            p.next = i1;
            i1.prev = p;
            i1 = i1.next;
        } else {
            p.next = i2;
            i2.prev = p;
            i2 = i2.next;
        }
    } else if(i1 != null) { // i1 != null && i2 == null
        p.next = i1;
        i1.prev = p;
        i1 = i1.next;
    } else { //i1 == null && i2 != null
        p.next = i2;
        i2.prev = p;
        i2 = i2.next;
    }
    p=p.next;
}

Per finire mettiamo a null l’ultimo riferimento, e restituiamo il primo nodo i:

p.next=null;
return i;

Questo era il caso ricorsivo. Nel caso base (i==f) non dobbiamo far altro che restituire l’unico elemento della lista (aggiornando i riferimenti per “staccare” la mini-lista dal resto della lista):

if(i==f) {
    i.prev = i.next = null;
    return i;
}
else {
    .... //Caso ricorsivo, visto in precedenza
}

Ed ora il metodo principale. Si noti che il metodo deve aggiornare i riferimenti first e last dell’oggetto di tipo ListaCollegata. first ci viene restituito “gratis” dal metodo ricorsivo, mentre last lo dobbiamo cercare attraverso una scansione della lista:

public void mergeSort() {
    if(first!=null) {
        ListNode i=mergeSortRic(first, last);
        first=i;
        while(i.next!=null)
            i=i.next;
        last=i;
    }
}

Misura sperimentale del costo dell’algoritmo

Ecco i metodi:

public static void riempiLista(ListaCollegata l, int n) {
    Random r=new Random();
    for(int i=0; i<n; i++)
        l.inserisciInCoda(r.nextInt());
}
 
public static long getTime(int dimLista, int n) {
    long tot=0;
    int i;
    for(i=0; i<n; i++) {
        ListaCollegata l=new ListaCollegata();
        riempiLista(l, dimLista);
        long start=System.currentTimeMillis();
        l.mergeSort();
        tot += (System.currentTimeMillis() - start);
    }
    return tot;
}
 
public static void main(String[] args) {
    long i;
    for(i=10; i<10000000; i*=10) {
        double t=getTime((int)i, 100);
        System.out.println(
            i + "\t"
            + t + "\t"
            + t/(i*Math.log(i)) + "\t"
            + t/(i*i)
        );
    }
}

Ed il risultato dell’esecuzione sulla mia macchina:

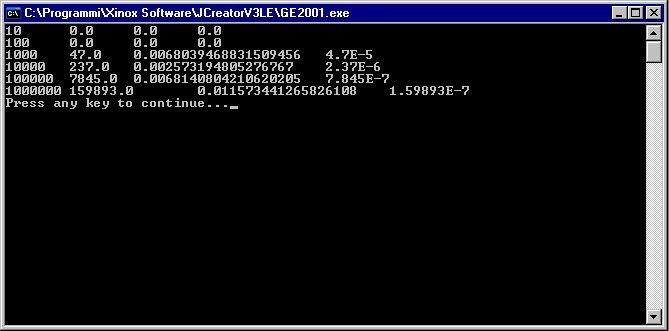
Si osservi come la penultima colonna () ha valori simili, mentre l’ultima colonna () ha valori che diminuiscono di quasi un ordine di grandezza ogni volta che aumenta di un ordine di grandezza.

Rimozione di duplicati

E’ sufficiente ordinare la lista, e poi scandirla una volta: gli elementi duplicati sono adiacenti, ed è facile eliminarli.

Commenti dei visitatori

Accedi per lasciare commenti.