» ASD » 2005-06 » 15/05/06

Seconda Esercitazione in Laboratorio

In questa esercitazione si chiede di:

scrivere una semplice classe che implementi una lista doppiamente collegata;
eseguire il MergeSort sulla lista, con costo $O(n \log n)$ ;
misurare sperimentalmente il costo dell’algoritmo;
applicare l’algoritmo alla trasformazione di un multiinsieme in un insieme.

Lista doppiamente collegata

Scrivere una classe ListaCollegata che implementi una lista doppiamente collegata di interi.

Per prima cosa, predisporre una classe ListNode (non pubblica) per rappresentare un nodo della lista (per semplicitÃ , usare solo variabili di istanza pubbliche nella classe).

Successivamente, scrivere la classe ListaCollegata che fornisca i metodi seguenti (si noti che si tratta soltanto dei metodi strettamente indispensabili per il prosieguo dell’esercitazione):

public ListaCollegata(): costruttore. Costruisce una nuova lista vuota.
public void inserisciInCoda(int i): aggiunge l’elemento i in coda alla lista.
public String toString(): restituisce una stringa che rappresenta il contenuto della lista sotto forma di sequenza di interi separati da virgole. (Useremo questo metodo per scopo di debugging.)

Scrivere un metodo main che costruisca e stampi la seguente lista: (5, 3, 5, 8, 2, 5, 3).

Ordinamento tramite MergeSort

Aggiungere alla classe ListaCollegata il metodo

public void mergeSort(): ordina la lista tramite l’algoritmo MergeSort, con costo $O(n \log n)$ .

L’algoritmo di MergeSort deve lavorare direttamente sulla lista. Non deve convertire la lista in array, applicare il MergeSort all’array e riconvertire l’array in lista. Naturalmente occorre modificare in modo opportuno il codice studiato a lezione, facendo attenzione a non incrementarne la complessitÃ asintotica.

Testare il metodo sulla lista creata in precedenza.

Misura sperimentale delle prestazioni dell’algoritmo

Misurare il costo computazionale $A(n)$ del metodo mergeSort in funzione della dimensione dell’input. Creare una tabella in cui si rapportino i tempi misurati con alcune funzioni matematiche, per esempio $n \log n$ e $n^2$ :

$n$	$A(n)$	$\frac{A(n)}{n \log n}$	$\frac{A(n)}{n^2}$
100	…	…	…
1000	…	…	…
10000	…	…	…
…	…	…	…

Per $n \rightarrow +\infty$ , si dovrebbe osservare che $\frac{A(n)}{n \log n}$ si stabilizza verso una costante, mentre $\frac{A(n)}{n^2} \rightarrow 0$ .

PoichÃ© per valori piccoli dell’input l’algoritmo Ã¨ molto veloce, Ã¨ difficile misurarne in modo preciso il costo. Si consiglia di ripetere l’esecuzione dell’algoritmo $k$ volte per ogni valore di $n$ . Si consiglia di scrivere ed impiegare i seguenti metodi:

public static void riempiLista(ListaCollegata l, int n): inserisce n interi generati a caso in coda alla lista l (utilizzare la classe java.util.Random() e il suo metodo nextInt());
public static long getTime(int n, int k): per k volte, genera una nuova lista di dimensione n e la ordina tramite mergeSort. Restituisce il tempo complessivo, in millisecondi, impiegato dalle k esecuzioni del mergeSort, avendo cura di escludere il costo della costruzione delle liste. Si suggerisce di fare ricorso al metodo statico System.currentTimeMillis().

Trasformare un multiinsieme in un insieme

Supponiamo che un multiinsieme $I$ sia rappresentato tramite lista concatenata. Ideare un algoritmo che trasformi $I$ in un insieme, rimuovendo gli elementi duplicati, con costo asintotico $O(n \log n)$ .

Suggerimenti

MergeSort

Per eseguire il passo merge del MergeSort si hanno almeno due possibilitÃ :

operare come nella versione “per array” del MergeSort: fondere le due liste ordinate in un oggetto temporaneo (per esempio in una nuova lista temporanea), e poi rimpiazzare gli elementi originali con quelli temporanei;
oppure, fondere le due liste semplicemente modificando i riferimenti.

In quest’ultimo caso, le due liste seguenti:

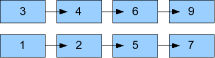
diventerebbero, semplicemente alterando i riferimenti:

Osserviamo che questa soluzione, oltre ad essere indubbiamente elegante, ha il pregio di non richiedere la copia di alcun oggetto (che puÃ² essere di grande utilitÃ nel caso in cui copiare un oggetto sia significativamente piÃ¹ costoso che confrontarlo con un altro oggetto), e di non richiedere spazio aggiuntivo.

Si noti che, cambiando i riferimenti, il primo e l’ultimo record della lista possono non essere gli stessi che si avevano in precedenza. Occorre gestire questa differenza, per fondere e collegare correttamente i vari spezzoni di lista.

Misura delle prestazioni

Prestare particolare attenzione ai tipi di dato con cui si rappresentano $n$ e il tempo. Ricordarsi che $n^2$ puÃ² essere molto grande e generare overflow: Ã¨ opportuno rappresentarlo tramite long o double. Ricordarsi, inoltre, che la “divisione” tra due interi Ã¨ il loro quoziente intero: a noi invece interessa il rapporto, quindi Ã¨ necessaria una divisione tra double (fare il cast di almeno un argomento).

Scegliere un valore opportuno di $k$ (a seconda della velocitÃ della macchina). Per esempio, $k=100$ Ã¨ un valore ragionevole per macchine recenti.

Commenti dei visitatori

Accedi per lasciare commenti.

Contents